1、3069. 将元素分配到两个数组中 I

给你一个下标从 1 开始、包含不同整数的数组 nums ，数组长度为 n 。

你需要通过 n 次操作，将 nums 中的所有元素分配到两个数组 arr1 和 arr2 中。在第一次操作中，将 nums[1] 追加到 arr1 。在第二次操作中，将 nums[2] 追加到 arr2 。之后，在第 i 次操作中：

如果 arr1 的最后一个元素大于 arr2 的最后一个元素，就将 nums[i] 追加到 arr1 。否则，将 nums[i] 追加到 arr2 。

通过连接数组 arr1 和 arr2 形成数组 result 。例如，如果 arr1 == [1,2,3] 且 arr2 == [4,5,6] ，那么 result = [1,2,3,4,5,6] 。

返回数组 result 。

示例 1：

1
2
3
4
5
6
输入：nums = [2,1,3]
输出：[2,3,1]
解释：在前两次操作后，arr1 = [2] ，arr2 = [1] 。
在第 3 次操作中，由于 arr1 的最后一个元素大于 arr2 的最后一个元素（2 > 1），将 nums[3] 追加到 arr1 。
3 次操作后，arr1 = [2,3] ，arr2 = [1] 。
因此，连接形成的数组 result 是 [2,3,1] 。

示例 2：

1
2
3
4
5
6
7
输入：nums = [5,4,3,8]
输出：[5,3,4,8]
解释：在前两次操作后，arr1 = [5] ，arr2 = [4] 。
在第 3 次操作中，由于 arr1 的最后一个元素大于 arr2 的最后一个元素（5 > 4），将 nums[3] 追加到 arr1 ，因此 arr1 变为 [5,3] 。
在第 4 次操作中，由于 arr2 的最后一个元素大于 arr1 的最后一个元素（4 > 3），将 nums[4] 追加到 arr2 ，因此 arr2 变为 [4,8] 。
4 次操作后，arr1 = [5,3] ，arr2 = [4,8] 。
因此，连接形成的数组 result 是 [5,3,4,8] 。

提示：

3 <= n <= 50
1 <= nums[i] <= 100
nums中的所有元素都互不相同。

没什么好说的，傻瓜题

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int[] resultArray(int[] nums) {
        int n=nums.length;
        List<Integer> a=new ArrayList<>();
        List<Integer> b=new ArrayList<>();
        a.add(nums[0]);
        b.add(nums[1]);
        for(int i=2;i<n;i++){
            if(a.get(a.size()-1)>b.get(b.size()-1)){
                a.add(nums[i]);
            }else{
                b.add(nums[i]);
            }
        }
        a.addAll(b);
        for(int i=0;i<n;i++){
            nums[i]=a.get(i);
        }
        return nums;
    }
}

如果可以，尽量加入rust解法

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
impl Solution{
    pub fn result_array(nums: Vec<i32>) -> Vec<i32>{
        let mut arr1=vec![];
        let mut arr2=vec![];
        arr1.push(nums[0]);
        arr2.push(nums[1]);
        let len=nums.len();
        for i in 2..len{
            if arr1.last().unwrap() > arr2.last().unwrap(){
                arr1.push(nums[i]);
            }else{
                arr2.push(nums[i]);
            }
        }
        arr1.extend_from_slice(&arr2);
        arr1
    }
}

2、3070. 元素和小于等于 k 的子矩阵的数目

给你一个下标从 0 开始的整数矩阵 grid 和一个整数 k。

返回包含 grid 左上角元素、元素和小于或等于 k 的 子矩阵的数目。

示例 1：

1
2
3
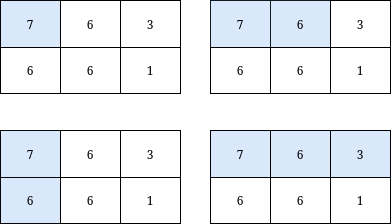
输入：grid = [[7,6,3],[6,6,1]], k = 18
输出：4
解释：如上图所示，只有 4 个子矩阵满足：包含 grid 的左上角元素，并且元素和小于或等于 18 。

示例 2：

1
2
3
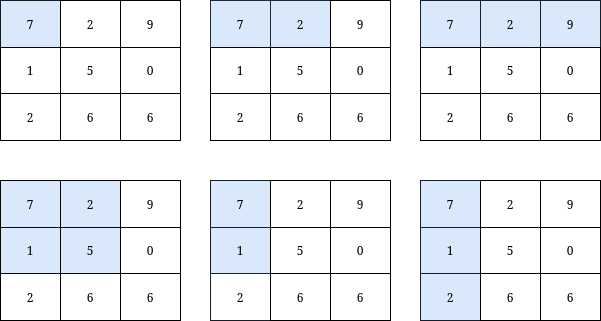
输入：grid = [[7,2,9],[1,5,0],[2,6,6]], k = 20
输出：6
解释：如上图所示，只有 6 个子矩阵满足：包含 grid 的左上角元素，并且元素和小于或等于 20 。

提示：

m == grid.length
n == grid[i].length
1 <= n, m <= 1000
0 <= grid[i][j] <= 1000
1 <= k <= 109

先是我当时的解法，计算第一列最多有多少满足条件的矩形，后面的每一列满足条件的列只能小于等于第一列，计算一共有多少满足条件的。

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class Solution {

    public int countSubmatrices(int[][] grid, int k) {
        //我的丑陋解法
        int res=0;
        if(grid[0][0]>k) return res;
        int[] n1=new int[grid.length];
        n1[0]=grid[0][0];
        res++;
        int t= grid.length-1;
        for(int i=1;i<grid.length;i++){
            n1[i]=n1[i-1]+grid[i][0];
            res++;
            if(n1[i]>k){
                t=i;
                res--;
                break;
            }
        }
        for(int i=1;i<grid[0].length&&n1[0]<=k;i++){
            int s=0;
            for(int j=0;j<=t;j++){
                s+=grid[j][i];
                n1[j]+=s;
                if(n1[j]<=k) res++;
                else {
                    t=j;
                    break;
                }
            }
        }
        return res;
    }

}

方法一：前缀和

如何求二维数组的前缀和

2024-3-1617:04:40-1710579879374.png

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
class Solution {
    public int countSubmatrices(int[][] grid, int k) {
        int res=0;
        int m=grid.length;
        int n=grid[0].length;
        int[][] sum=new int[m+1][n+1];
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                // 到当前元素左上的二维数组和=左边为止的和+上边为止的和-左上方为止的和+当前元素的大小
                sum[i+1][j+1]=sum[i+1][j]+sum[i][j+1]-sum[i][j]+grid[i][j];
                if(sum[i+1][j+1]<=k) res++;
            }
        }
        return res;
    }
}

方法二：维护每列的元素和

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
class Solution {
    public int countSubmatrices(int[][] grid, int k) {
        int res=0;
        int n=grid[0].length;
        // 记录每一列的大小
        int[] nums=new int[n];
        for(int[] num:grid){
            // 每一行开始计算时，初始化大小为0
            int s=0;
            for(int j=0;j<n;j++){
                // 当前行的大小=上一行时的大小+当前元素的大小
                nums[j]+=num[j];
                // 目前的和为上一列的大小+当前列的大小
                s+=nums[j];
                if(s>k) break;
                res++;
            }
        }
        return res;
    }
}

3、3071. 在矩阵上写出字母 Y 所需的最少操作次数

给你一个下标从 0 开始、大小为 n x n 的矩阵 grid ，其中 n 为奇数，且 grid[r][c] 的值为 0 、1 或 2 。

如果一个单元格属于以下三条线中的任一一条，我们就认为它是字母 Y 的一部分：

从左上角单元格开始到矩阵中心单元格结束的对角线。
从右上角单元格开始到矩阵中心单元格结束的对角线。
从中心单元格开始到矩阵底部边界结束的垂直线。

当且仅当满足以下全部条件时，可以判定矩阵上写有字母 Y ：

属于 Y 的所有单元格的值相等。
不属于 Y 的所有单元格的值相等。
属于 Y 的单元格的值与不属于Y的单元格的值不同。

每次操作你可以将任意单元格的值改变为 0 、1 或 2 。返回在矩阵上写出字母 Y 所需的最少操作次数。

示例 1：

1
2
3
4
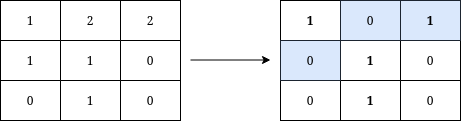
输入：grid = [[1,2,2],[1,1,0],[0,1,0]]
输出：3
解释：将在矩阵上写出字母 Y 需要执行的操作用蓝色高亮显示。操作后，所有属于 Y 的单元格（加粗显示）的值都为 1 ，而不属于 Y 的单元格的值都为 0 。
可以证明，写出 Y 至少需要进行 3 次操作。

示例 2：

1
2
3
4
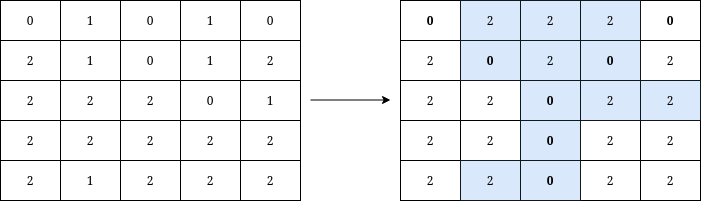
输入：grid = [[0,1,0,1,0],[2,1,0,1,2],[2,2,2,0,1],[2,2,2,2,2],[2,1,2,2,2]]
输出：12
解释：将在矩阵上写出字母 Y 需要执行的操作用蓝色高亮显示。操作后，所有属于 Y 的单元格（加粗显示）的值都为 0 ，而不属于 Y 的单元格的值都为 2 。
可以证明，写出 Y 至少需要进行 12 次操作。

提示：

3 <= n <= 49
n == grid.length == grid[i].length
0 <= grid[i][j] <= 2
n 为奇数。

统计每种数字出现的次数，计算最多可以保留多少个元素不被修改，然后用元素的总数量减去保留的元素

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
class Solution {
    public int minimumOperationsToWriteY(int[][] grid) {
        // 和茶神想法一样，但就是菜没做出来
        int[] t1=new int[3];
        int[] t2=new int[3];
        for(int i=0;i<grid.length/2;i++){
            for(int j=0;j<grid.length;j++){
                if(i==j||i==grid.length-1-j){
                    t1[grid[i][j]]++;
                } else{
                    t2[grid[i][j]]++;
                }
            }
        }
        for(int i=grid.length/2;i<grid.length;i++){
            for(int j=0;j<grid.length;j++){
                if(j==grid.length/2) t1[grid[i][j]]++;
                else t2[grid[i][j]]++;
            }
        }
        int res=0;
        for(int i=0;i<3;i++){
            for(int j=0;j<3;j++){
                if(i!=j){
                    res=Math.max(res,t1[i]+t2[j]);
                }
            }
        }
        return grid.length*grid[0].length-res;
    }
}

4、3072. 将元素分配到两个数组中 II

困难

给你一个下标从 1 开始、长度为 n 的整数数组 nums 。

现定义函数 greaterCount ，使得 greaterCount(arr, val) 返回数组 arr 中 严格大于 val 的元素数量。

你需要使用 n 次操作，将 nums 的所有元素分配到两个数组 arr1 和 arr2 中。在第一次操作中，将 nums[1] 追加到 arr1 。在第二次操作中，将 nums[2] 追加到 arr2 。之后，在第 i 次操作中：

如果 greaterCount(arr1, nums[i]) > greaterCount(arr2, nums[i]) ，将 nums[i] 追加到 arr1 。
如果 greaterCount(arr1, nums[i]) < greaterCount(arr2, nums[i]) ，将 nums[i] 追加到 arr2 。
如果 greaterCount(arr1, nums[i]) == greaterCount(arr2, nums[i]) ，将 nums[i] 追加到元素数量较少的数组中。
如果仍然相等，那么将 nums[i] 追加到 arr1 。

连接数组 arr1 和 arr2 形成数组 result 。例如，如果 arr1 == [1,2,3] 且 arr2 == [4,5,6] ，那么 result = [1,2,3,4,5,6] 。

返回整数数组 result 。

示例 1：

1
2
3
4
5
6
7
输入：nums = [2,1,3,3]
输出：[2,3,1,3]
解释：在前两次操作后，arr1 = [2] ，arr2 = [1] 。
在第 3 次操作中，两个数组中大于 3 的元素数量都是零，并且长度相等，因此，将 nums[3] 追加到 arr1 。
在第 4 次操作中，两个数组中大于 3 的元素数量都是零，但 arr2 的长度较小，因此，将 nums[4] 追加到 arr2 。
在 4 次操作后，arr1 = [2,3] ，arr2 = [1,3] 。
因此，连接形成的数组 result 是 [2,3,1,3] 。

示例 2：

1
2
3
4
5
6
7
8
输入：nums = [5,14,3,1,2]
输出：[5,3,1,2,14]
解释：在前两次操作后，arr1 = [5] ，arr2 = [14] 。
在第 3 次操作中，两个数组中大于 3 的元素数量都是一，并且长度相等，因此，将 nums[3] 追加到 arr1 。
在第 4 次操作中，arr1 中大于 1 的元素数量大于 arr2 中的数量（2 > 1），因此，将 nums[4] 追加到 arr1 。
在第 5 次操作中，arr1 中大于 2 的元素数量大于 arr2 中的数量（2 > 1），因此，将 nums[5] 追加到 arr1 。
在 5 次操作后，arr1 = [5,3,1,2] ，arr2 = [14] 。
因此，连接形成的数组 result 是 [5,3,1,2,14] 。

示例 3：

1
2
3
4
输入：nums = [3,3,3,3]
输出：[3,3,3,3]
解释：在 4 次操作后，arr1 = [3,3] ，arr2 = [3,3] 。
因此，连接形成的数组 result 是 [3,3,3,3] 。

提示：

3 <= n <= 105
1 <= nums[i] <= 109

抄了茶神的树状数组，但是太复杂了，一遍听懂，过后就忘

题解地址：（后续专门来学习树状数组）

307. 区域和检索 - 数组可修改 - 力扣（LeetCode）

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
class Fenwick{
    private final int[] tree;

    public Fenwick(int n){
        tree=new int[n];
    }

    // 把下标为i的元素增加v
    public void add(int i,int v){
        while(i<tree.length){
            tree[i]+=v;
            // 求lowbit
            i+=i&-i;
        }
    }

//  返回下标在【1，i】的元素之和
    public int pre(int i){
        int res=0;
        while(i>0){
            res+=tree[i];
//          这个有点复杂
            i&=i-1;
        }
        return res;
    }
}

class Solution {
    public int[] resultArray(int[] nums) {
        // 抄了茶神的树状数组，暂时听懂了，但自己操作还是搞不来
        int[] sorted=nums.clone();
        Arrays.sort(sorted);//没有去重的排序
        int n=nums.length;
        List<Integer> a=new ArrayList<>(n);
        List<Integer> b=new ArrayList<>();
        a.add(nums[0]);
        b.add(nums[1]);
        Fenwick t=new Fenwick(n+1);
        t.add(n-Arrays.binarySearch(sorted,nums[0]),1);
        t.add(n-Arrays.binarySearch(sorted,nums[1]),-1);

        for(int i=2;i<nums.length;i++){
            int x=nums[i];
            int v=n-Arrays.binarySearch(sorted,x);
            int d=t.pre(v-1);  //转换成<v的元素个数之差
            if(d>0||d==0&&a.size()<=b.size()){
                a.add(x);
                t.add(v,1);
            }else{
                b.add(x);
                t.add(v,-1);
            }
        }
        a.addAll(b);
        for(int i=0;i<n;i++){
            nums[i]=a.get(i);
        }
        return nums;
    }
}