简单
给你一个整数数组 nums 。
返回满足 nums[i] 的数位和(每一位数字相加求和)等于 i 的 最小 下标 i 。
如果不存在满足要求的下标,返回 -1 。
示例 1:
**输入:**nums = [1,3,2]
**输出:**2
解释:
nums[2] = 2,其数位和等于 2 ,与其下标 i = 2 相等。因此,输出为 2 。
示例 2:
**输入:**nums = [1,10,11]
**输出:**1
解释:
nums[1] = 10,其数位和等于 1 + 0 = 1,与其下标 i = 1 相等。nums[2] = 11,其数位和等于是 1 + 1 = 2,与其下标 i = 2 相等。- 由于下标 1 是满足要求的最小下标,输出为 1 。
示例 3:
**输入:**nums = [1,2,3]
输出:-1
解释:
提示:
1 <= nums.length <= 1000 <= nums[i] <= 1000
解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
| impl Solution {
pub fn smallest_index(nums: Vec<i32>) -> i32 {
for (i, &num) in nums.iter().enumerate() {
let mut t = num;
let mut r = 0;
while t > 0 {
r += t % 10;
t /= 10;
}
if r == i as i32 {
return i as i32;
}
}
-1
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
| class Solution {
public int smallestIndex(int[] nums) {
for(int i=0;i<nums.length;i++){
int t=nums[i],r=0;
while(t>0){
r+=t%10;
t/=10;
}
if(r==i) return i;
}
return -1;
}
}
|
中等
给你一个由 互不相同 的正整数组成的数组 nums,需要根据每个数字的数位和(即每一位数字相加求和)按 升序 对数组进行排序。如果两个数字的数位和相等,则较小的数字排在前面。
返回将 nums 排列为上述排序顺序所需的 最小 交换次数。
一次 交换 定义为交换数组中两个不同位置的值。
示例 1:
输入: nums = [37,100]
输出: 1
解释:
- 计算每个整数的数位和:
[3 + 7 = 10, 1 + 0 + 0 = 1] → [10, 1] - 根据数位和排序:
[100, 37]。将 37 与 100 交换,得到排序后的数组。 - 因此,将
nums 排列为排序顺序所需的最小交换次数为 1。
示例 2:
输入: nums = [22,14,33,7]
输出: 0
解释:
- 计算每个整数的数位和:
[2 + 2 = 4, 1 + 4 = 5, 3 + 3 = 6, 7 = 7] → [4, 5, 6, 7] - 根据数位和排序:
[22, 14, 33, 7]。数组已经是排序好的。 - 因此,将
nums 排列为排序顺序所需的最小交换次数为 0。
示例 3:
输入: nums = [18,43,34,16]
输出: 2
解释:
- 计算每个整数的数位和:
[1 + 8 = 9, 4 + 3 = 7, 3 + 4 = 7, 1 + 6 = 7] → [9, 7, 7, 7] - 根据数位和排序:
[16, 34, 43, 18]。将 18 与 16 交换,再将 43 与 34 交换,得到排序后的数组。 - 因此,将
nums 排列为排序顺序所需的最小交换次数为 2。
提示:
1 <= nums.length <= 1051 <= nums[i] <= 109nums 由 互不相同 的正整数组成。
解
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
| class Solution {
public int minSwaps(int[] nums) {
int[][] tt=new int[nums.length][2];
for(int i=0;i<nums.length;i++){
int t=nums[i];
int r=0;
while(t>0){
r+=t%10;
t/=10;
}
tt[i][0]=r;
tt[i][1]=i;
}
Arrays.sort(tt,(a,b)->{
if(a[0]==b[0]) return nums[a[1]]-nums[b[1]];
return a[0]-b[0];
});
int res=0;
for(int i=0;i<nums.length;i++){
int t=tt[i][1];
while(t!=i){
int t1=tt[t][1];
tt[t][1]=t;
t=t1;
res++;
}
}
return res;
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| impl Solution {
pub fn min_swaps(nums: Vec<i32>) -> i32 {
let mut tt: Vec<(i32, usize)> = nums
.iter()
.enumerate()
.map(|(i, &num)| {
let mut t = num;
let mut r = 0;
while t > 0 {
r += t % 10;
t /= 10;
}
(r, i)
})
.collect();
// 排序逻辑
tt.sort_by(|a, b| {
if a.0 == b.0 {
nums[a.1].cmp(&nums[b.1])
} else {
a.0.cmp(&b.0)
}
});
let mut res = 0;
let mut visited = vec![false; nums.len()];
// 计算交换次数
for i in 0..nums.len() {
if visited[i] || tt[i].1 == i {
continue;
}
let mut cycle_size = 0;
let mut t = i;
while !visited[t] {
visited[t] = true;
t = tt[t].1;
cycle_size += 1;
}
if cycle_size > 1 {
res += cycle_size - 1;
}
}
res
}
}
|
多个元素相互站位的情况表示存在环(联通块),则排序这些联通块一定可以少排一次,因为联通块中的最后一个元素不需要在排列了,之前其他元素排序时,迫使最后一个元素已经到了正确的位置上。所有最终答案就等于元素总数-联通块的数量。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
| class Solution {
// 并查集模板
class UnionFind {
int[] tt;
int[] ss;
// 记录联通块的数量
int cc;
public UnionFind(int n) {
tt=new int[n];
for(int i=0;i<n;i++){
tt[i]=i;
}
ss=new int[n];
cc=n;
}
public int find(int x){
if(tt[x]!=x) tt[x]=find(tt[x]);
return tt[x];
}
public void union(int x, int y){
int a=find(x);
int b=find(y);
if(a==b) return;
if(ss[a]<ss[b]){
tt[a]=b;
}else if (ss[a]>ss[b]){
tt[b]=a;
}else{
tt[b]=a;
ss[a]++;
}
cc--;
}
}
public int minSwaps(int[] nums) {
int n=nums.length;
int[][] a=new int[n][3];
for (int i = 0; i < n; i++) {
// 初始化
int s=0;
for(int x=nums[i];x>0;x/=10){
s+=x%10;
}
// 值
a[i][0]=s;
// 原始值
a[i][1]=nums[i];
// 下标
a[i][2]=i;
}
// 按照题意排序
Arrays.sort(a,(x,y)->x[0]!=y[0]?x[0]-y[0]:x[1]-y[1]);
// 新建并查集
UnionFind u = new UnionFind(n);
for (int i = 0; i < n; i++) {
// 让下标与联通块来连接
u.union(i,a[i][2]);
}
// 如果被联通了的联通块,可以少放置一次
return n-u.cc;
}
}
|
中等
给你一个大小为 m x n 的二维字符网格 matrix,用字符串数组表示,其中 matrix[i][j] 表示第 i 行和第 j 列处的单元格。每个单元格可以是以下几种字符之一:
'.' 表示一个空单元格。'#' 表示一个障碍物。- 一个大写字母(
'A' 到 'Z')表示一个传送门。
你从左上角单元格 (0, 0) 出发,目标是到达右下角单元格 (m - 1, n - 1)。你可以从当前位置移动到相邻的单元格(上、下、左、右),移动后的单元格必须在网格边界内且不是障碍物**。**
如果你踏入一个包含传送门字母的单元格,并且你之前没有使用过该传送门字母,你可以立即传送到网格中另一个具有相同字母的单元格。这次传送不计入移动次数,但每个字母对应的传送门在旅程中 最多 只能使用一次。
返回到达右下角单元格所需的 最少 移动次数。如果无法到达目的地,则返回 -1。
示例 1:
输入: matrix = [“A..”,".A.","…"]
输出: 2
解释:
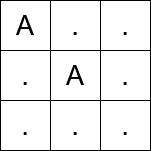
- 在第一次移动之前,从
(0, 0) 传送到 (1, 1)。 - 第一次移动,从
(1, 1) 移动到 (1, 2)。 - 第二次移动,从
(1, 2) 移动到 (2, 2)。
示例 2:
输入: matrix = [".#…",".#.#.",".#.#.","…#."]
输出: 13
解释:
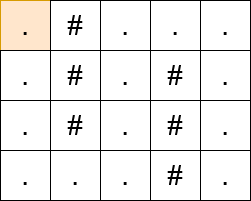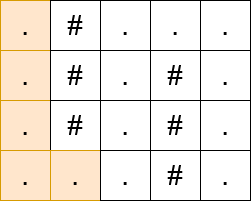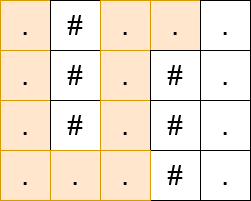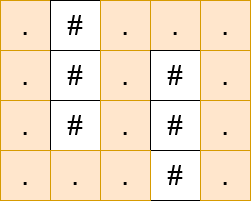
提示:
1 <= m == matrix.length <= 1031 <= n == matrix[i].length <= 103matrix[i][j] 是 '#'、'.' 或一个大写英文字母。matrix[0][0] 不是障碍物。

