关于并查集原理解析和练习题单
并查集原理
什么是并查集?
数据来源
并查集是一种用于管理元素所属集合的数据结构,实现为一个森林,其中每棵树表示一个集合,树中的节点表示对应集合中的元素。
- 合并:合并两个元素所属的集合
- 查询:查询某个元素所属集合,这可以用于判断两个元素是否属于同一集合。
初始化
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
| import java.util.stream.IntStream;
import java.util.Arrays;
class DSU {
private int[] pa;
public DSU(int size) {
//给元素赋值
pa = IntStream.range(0, size).toArray();
}
public int[] getPa() {
获取元素
return Arrays.copyOf(pa, pa.length);
}
}
|
查询
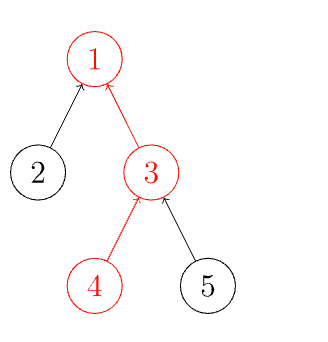
查找某个元素,一直向上搜索,直到找到对应的根节点。(同一组集合属于同一个根节点)
1
2
3
4
5
6
7
8
| public int find(int x) {
if (pa[x] == x) {
return x;
} else {
pa[x] = find(pa[x]); // 路径压缩
return pa[x];
}
}
|
合并
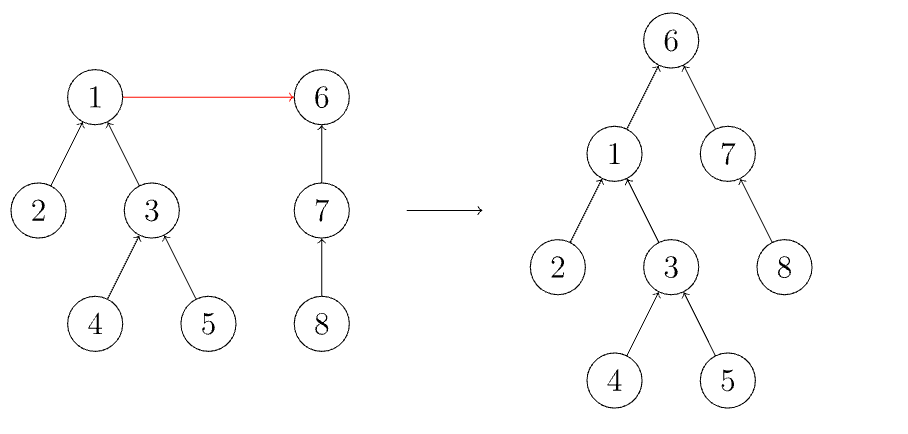
将一个树的根节合并到另一个树的根节点
1
2
3
| public void unite(int x, int y) {
pa[find(x)] = find(y);
}
|
删除
删除一个叶子节点的方式就是将被删除节点的父节点设置为自己。
为了保证要删除的元素都是叶子,我们可以预先为每个节点制作副本,并将其副本作为父亲。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
| import java.util.stream.IntStream;
import java.util.Arrays;
class DSU {
private int[] pa;
private int[] size;
// 构造函数
public DSU(int size_) {
int fullSize = size_ * 2;
pa = new int[fullSize];
size = new int[fullSize];
Arrays.fill(size, 1); // 初始化大小为1
IntStream.range(0, size_).forEach(i -> pa[i] = size_ + i);
IntStream.range(size_, fullSize).forEach(i -> pa[i] = i);
}
// 查找操作 (带路径压缩)
public int find(int x) {
if (pa[x] != x) {
pa[x] = find(pa[x]); // 路径压缩
}
return pa[x];
}
// 删除操作
public void erase(int x) {
int root = find(x);//找出被删除节点的父集合
size[root]--; // 减少根的大小计数
pa[x] = x; // 将自身重置为根
}
}
|
移动
一边增加一边减少
1
2
3
4
5
6
7
8
9
10
| public void move(int x, int y) {
int fx = find(x);
int fy = find(y);
if (fx == fy) {
return;
}
pa[x] = fy;
size[fx]--;
size[fy]++;
}
|
例题
困难
给你一个下标从 0 开始的整数数组 nums ,你可以在一些下标之间遍历。对于两个下标 i 和 j(i != j),当且仅当 gcd(nums[i], nums[j]) > 1 时,我们可以在两个下标之间通行,其中 gcd 是两个数的 最大公约数 。
你需要判断 nums 数组中 任意 两个满足 i < j 的下标 i 和 j ,是否存在若干次通行可以从 i 遍历到 j 。
如果任意满足条件的下标对都可以遍历,那么返回 true ,否则返回 false 。
示例 1:
1
2
3
4
5
| 输入:nums = [2,3,6]
输出:true
解释:这个例子中,总共有 3 个下标对:(0, 1) ,(0, 2) 和 (1, 2) 。
从下标 0 到下标 1 ,我们可以遍历 0 -> 2 -> 1 ,我们可以从下标 0 到 2 是因为 gcd(nums[0], nums[2]) = gcd(2, 6) = 2 > 1 ,从下标 2 到 1 是因为 gcd(nums[2], nums[1]) = gcd(6, 3) = 3 > 1 。
从下标 0 到下标 2 ,我们可以直接遍历,因为 gcd(nums[0], nums[2]) = gcd(2, 6) = 2 > 1 。同理,我们也可以从下标 1 到 2 因为 gcd(nums[1], nums[2]) = gcd(3, 6) = 3 > 1 。
|
示例 2:
1
2
3
| 输入:nums = [3,9,5]
输出:false
解释:我们没法从下标 0 到 2 ,所以返回 false 。
|
示例 3:
1
2
3
| 输入:nums = [4,3,12,8]
输出:true
解释:总共有 6 个下标对:(0, 1) ,(0, 2) ,(0, 3) ,(1, 2) ,(1, 3) 和 (2, 3) 。所有下标对之间都存在可行的遍历,所以返回 true 。
|
提示:
1 <= nums.length <= 105
1 <= nums[i] <= 105
java
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
| class Solution {
public boolean canTraverseAllPairs(int[] nums) {
// 过滤特殊情况
if(nums.length==1) return true;
// 默认大小可以包含所有数字
Demo demo=new Demo(100001);
for (int num : nums) {
// 如果有1一定不能走
if(num==1) return false;
// 求出所有非1的因子
for(int i=2;i*i<=num;i++){
if(num%i==0){
demo.union(num,i);
demo.union(num,num/i);
}
}
}
// 检查每次联通量是否相等
int p=0;
for (int num : nums) {
// 找出当前数字的联通量
int t = demo.find(num);
if(p==0){
p=t;
continue;
}
// 联通量不同
if(p!=t) return false;
}
return true;
}
class Demo{
// 记录每个数字的联通量
private int[] nums;
// 记录每个数字的大小,方便连接(小支连到大支)
private int[] ss;
// 初始化
public Demo(int s){
nums = new int[s];
for(int i=0;i<nums.length;i++){
nums[i] = i;
}
ss = new int[nums.length];
}
// 计算每个数字的联通量
public int find(int target){
// 当前节点就是根节点
if(nums[target]==target) return target;
// 不是就找到根
nums[target] = find(nums[target]);
return nums[target];
}
// 联通x和y两个节点
public void union(int x,int y){
// 分别找出每个节点的联通量
int a=find(x);
int b=find(y);
// 如果联通量相等,表示已经被连接
if(a==b) return;
// 小支联通大支
if(ss[a]<ss[b]){
nums[a]=b;
}else if (ss[b]<ss[a]){
nums[b]=a;
}else{
// 两个集合相等,默认a连接b,b的集合大小+1
nums[a]=b;
ss[b]++;
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
| struct DSU {
nums: Vec<usize>, // 每个数字的联通量
ss: Vec<usize>, // 每个集合的大小
}
impl DSU {
// 初始化
fn new(size: usize) -> Self {
DSU {
nums: (0..size).collect(),
ss: vec![0; size],
}
}
// 查找操作,路径压缩
fn find(&mut self, target: usize) -> usize {
if self.nums[target] != target {
self.nums[target] = self.find(self.nums[target]);
}
self.nums[target]
}
// 联通两个节点
fn union(&mut self, x: usize, y: usize) {
let a = self.find(x);
let b = self.find(y);
if a == b {
return;
}
if self.ss[a] < self.ss[b] {
self.nums[a] = b;
} else if self.ss[a] > self.ss[b] {
self.nums[b] = a;
} else {
self.nums[a] = b;
self.ss[b] += 1;
}
}
}
struct Solution;
impl Solution {
// 主逻辑
pub fn can_traverse_all_pairs(nums: Vec<usize>) -> bool {
// 过滤特殊情况
if nums.len() == 1 {
return true;
}
let mut dsu = DSU::new(100001);
for &num in &nums {
// 如果有 1,无法遍历
if num == 1 {
return false;
}
// 求出所有非 1 的因子
let mut i = 2;
while i * i <= num {
if num % i == 0 {
dsu.union(num, i);
dsu.union(num, num / i);
}
i += 1;
}
}
// 检查每次联通量是否相等
let mut p = 0;
for &num in &nums {
let t = dsu.find(num);
if p == 0 {
p = t;
continue;
}
if p != t {
return false;
}
}
true
}
}
|
困难
有 n 座城市,编号从 1 到 n 。编号为 x 和 y 的两座城市直接连通的前提是: x 和 y 的公因数中,至少有一个 严格大于 某个阈值 threshold 。更正式地说,如果存在整数 z ,且满足以下所有条件,则编号 x 和 y 的城市之间有一条道路:
x % z == 0y % z == 0z > threshold
给你两个整数 n 和 threshold ,以及一个待查询数组,请你判断每个查询 queries[i] = [ai, bi] 指向的城市 ai 和 bi 是否连通(即,它们之间是否存在一条路径)。
返回数组 answer ,其中answer.length == queries.length 。如果第 i 个查询中指向的城市 ai 和 bi 连通,则 answer[i] 为 true ;如果不连通,则 answer[i] 为 false 。
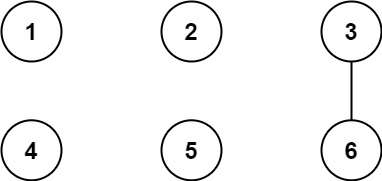
示例 1:
1
2
3
4
5
6
7
8
9
10
11
12
13
| 输入:n = 6, threshold = 2, queries = [[1,4],[2,5],[3,6]]
输出:[false,false,true]
解释:每个数的因数如下:
1: 1
2: 1, 2
3: 1, 3
4: 1, 2, 4
5: 1, 5
6: 1, 2, 3, 6
所有大于阈值的的因数已经加粗标识,只有城市 3 和 6 共享公约数 3 ,因此结果是:
[1,4] 1 与 4 不连通
[2,5] 2 与 5 不连通
[3,6] 3 与 6 连通,存在路径 3--6
|
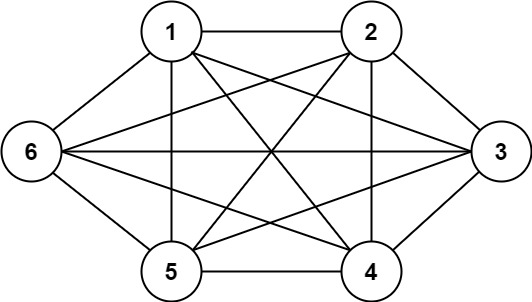
示例 2:
1
2
3
| 输入:n = 6, threshold = 0, queries = [[4,5],[3,4],[3,2],[2,6],[1,3]]
输出:[true,true,true,true,true]
解释:每个数的因数与上一个例子相同。但是,由于阈值为 0 ,所有的因数都大于阈值。因为所有的数字共享公因数 1 ,所以所有的城市都互相连通。
|
示例 3:
1
2
3
4
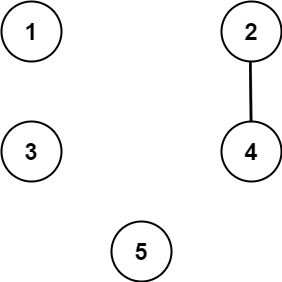
| 输入:n = 5, threshold = 1, queries = [[4,5],[4,5],[3,2],[2,3],[3,4]]
输出:[false,false,false,false,false]
解释:只有城市 2 和 4 共享的公约数 2 严格大于阈值 1 ,所以只有这两座城市是连通的。
注意,同一对节点 [x, y] 可以有多个查询,并且查询 [x,y] 等同于查询 [y,x] 。
|
提示:
2 <= n <= 1040 <= threshold <= n1 <= queries.length <= 105queries[i].length == 21 <= ai, bi <= citiesai != bi
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| class Solution {
public List<Boolean> areConnected(int n, int threshold, int[][] queries) {
Demo demo=new Demo(n+1);
// 联通所有满足条件的因子
for(int z=threshold+1;z<=n;z++){
for(int p=z,q=z*2;q<=n;p+=z,q+=z){
demo.union(p,q);
}
}
List<Boolean> res=new ArrayList<>();
for (int[] query : queries) {
res.add(demo.find(query[0])==demo.find(query[1]));
}
return res;
}
class Demo{
int[] nums;
int[] ss;
public Demo(int s) {
nums = new int[s];
for (int i = 0; i < s; i++) {
nums[i] = i;
}
ss = new int[s];
}
public int find(int t){
if(nums[t]!=t) nums[t] = find(nums[t]);
return nums[t];
}
public void union(int x, int y){
int a=find(x);
int b=find(y);
if(a==b) return;
if(ss[a]<ss[b]){
nums[a]=b;
}else if (ss[b]<ss[a]){
nums[b]=a;
}else{
nums[b]=a;
ss[a]++;
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
| use std::iter::repeat_with;
struct UnionFind{
parent: Vec<i32>,
size: Vec<i32>,
n: i32,
}
impl UnionFind {
fn new(n:i32)-> Self{
let mut parent: Vec<i32>=(0..n).collect();
let size =vec![1; n as usize];
UnionFind{parent,size,n}
}
fn findset(&mut self,x: i32)-> i32{
if(self.parent[x as usize] !=x){
self.parent[x as usize]= self.findset(self.parent[x as usize]);
}
self.parent[x as usize]
}
fn unite(&mut self, mut x: i32,mut y: i32){
x=self.findset(x);
y=self.findset(y);
if x!=y{
if(self.size[x as usize] <self.size[y as usize] ){
std::mem::swap(&mut x,&mut y);
}
self.parent[y as usize]=x;
self.size[x as usize]+=self.size[y as usize];
}
}
fn connected(&mut self,x:i32,y: i32)-> bool{
self.findset(x)==self.findset(y)
}
}
impl Solution {
pub fn are_connected(n: i32, threshold: i32, queries: Vec<Vec<i32>>) -> Vec<bool> {
let mut uf =UnionFind::new(n+1);
let mut is_prime=vec![true;(n+1) as usize];
for z in(threshold+1)..=n{
if is_prime[z as usize]{
let mut p=z;
let mut q=z*2;
while(q<=n){
uf.unite(p,q);
is_prime[q as usize]=false;
p+=z;
q+=z;
}
}
}
queries.into_iter().map(|q| uf.connected(q[0],q[1])).collect()
}
}
//runtime:3 ms
//memory:8.6 MB
|
困难
给定一个由不同正整数的组成的非空数组 nums ,考虑下面的图:
- 有
nums.length 个节点,按从 nums[0] 到 nums[nums.length - 1] 标记; - 只有当
nums[i] 和 nums[j] 共用一个大于 1 的公因数时,nums[i] 和 nums[j]之间才有一条边。
返回 图中最大连通组件的大小 。
示例 1:

1
2
| 输入:nums = [4,6,15,35]
输出:4
|
示例 2:

1
2
| 输入:nums = [20,50,9,63]
输出:2
|
示例 3:

1
2
| 输入:nums = [2,3,6,7,4,12,21,39]
输出:8
|
提示:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| class Solution {
public int largestComponentSize(int[] nums) {
int res=0;
Demo demo=new Demo(100001);
for (int num : nums) {
for(int t=2;t*t<=num;t++){
if(num%t!=0) continue;
demo.union(num,t);
demo.union(t,num/t);
}
}
int[] tt=new int[100001];
for (int num : nums) {
int t=demo.find(num);
tt[t]++;
res=Math.max(res,tt[t]);
}
return res;
}
class Demo{
int[] nums;
int[] ss;
public Demo(int s){
nums = new int[s];
for (int i = 0; i < nums.length; i++) {
nums[i] = i;
}
ss = new int[s];
}
public int find(int t){
if(nums[t]!=t){
nums[t]=find(nums[t]);
}
return nums[t];
}
public void union(int x,int y){
int a=find(x);
int b=find(y);
if(a==b) return ;
if(ss[a]<ss[b]){
nums[a]=b;
}else if(ss[a]>ss[b]){
nums[b]=a;
}else{
nums[b]=a;
ss[a]++;
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
| struct DSU {
nums: Vec<usize>, // 每个数字的父节点,用于记录连通分量
ss: Vec<usize>, // 每个集合的大小,用于优化合并
}
impl DSU {
// 初始化 DSU
fn new(size: usize) -> Self {
DSU {
nums: (0..size).collect(), // 初始化父节点为自身
ss: vec![0; size], // 初始化所有集合大小为 0
}
}
// 查找操作,带路径压缩
fn find(&mut self, t: usize) -> usize {
if self.nums[t] != t {
self.nums[t] = self.find(self.nums[t]); // 路径压缩
}
self.nums[t]
}
// 合并两个集合,按秩合并
fn union(&mut self, x: usize, y: usize) {
let a = self.find(x);
let b = self.find(y);
if a == b {
return; // 已经在同一个集合
}
if self.ss[a] < self.ss[b] {
self.nums[a] = b;
} else if self.ss[a] > self.ss[b] {
self.nums[b] = a;
} else {
self.nums[b] = a;
self.ss[a] += 1; // 增加根节点 a 的秩
}
}
}
struct Solution;
impl Solution {
// 主函数:计算最大的连通分量的大小
pub fn largest_component_size(nums: Vec<usize>) -> usize {
let mut res = 0;
let mut dsu = DSU::new(100001);
// 遍历 nums,将每个数字与它的因子合并
for &num in &nums {
let mut t = 2;
while t * t <= num {
if num % t == 0 {
dsu.union(num, t); // 合并 num 和因子 t
dsu.union(t, num / t); // 合并因子 t 和 num/t
}
t += 1;
}
}
let mut counts = vec![0; 100001]; // 记录每个连通分量的大小
// 遍历 nums,统计每个连通分量的大小
for &num in &nums {
let root = dsu.find(num); // 找到 num 的根节点
counts[root] += 1; // 增加根节点对应的连通分量大小
res = res.max(counts[root]); // 更新最大连通分量大小
}
res
}
}
|
困难
给你一个整数数组 nums ,你可以在 nums 上执行下述操作 任意次 :
- 如果
gcd(nums[i], nums[j]) > 1 ,交换 nums[i] 和 nums[j] 的位置。其中 gcd(nums[i], nums[j]) 是 nums[i] 和 nums[j] 的最大公因数。
如果能使用上述交换方式将 nums 按 非递减顺序 排列,返回 true ;否则,返回 false 。
示例 1:
1
2
3
4
5
| 输入:nums = [7,21,3]
输出:true
解释:可以执行下述操作完成对 [7,21,3] 的排序:
- 交换 7 和 21 因为 gcd(7,21) = 7 。nums = [21,7,3]
- 交换 21 和 3 因为 gcd(21,3) = 3 。nums = [3,7,21]
|
示例 2:
1
2
3
| 输入:nums = [5,2,6,2]
输出:false
解释:无法完成排序,因为 5 不能与其他元素交换。
|
示例 3:
1
2
3
4
5
6
7
| 输入:nums = [10,5,9,3,15]
输出:true
解释:
可以执行下述操作完成对 [10,5,9,3,15] 的排序:
- 交换 10 和 15 因为 gcd(10,15) = 5 。nums = [15,5,9,3,10]
- 交换 15 和 3 因为 gcd(15,3) = 3 。nums = [3,5,9,15,10]
- 交换 10 和 15 因为 gcd(10,15) = 5 。nums = [3,5,9,10,15]
|
提示:
1 <= nums.length <= 3 * 1042 <= nums[i] <= 105
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
| class Solution {
public boolean gcdSort(int[] nums) {
int[] sort =nums.clone();
Arrays.sort(sort);
UnionFind uf=new UnionFind(sort[nums.length-1]+1);
for (int num : nums) {
int cur =num;
for(int t=2;t*t<=num;t++){
if(num%t==0){
uf.union(cur,t);
if(num/t>1) uf.union(cur,num/t);
}
}
}
for (int i = 0; i < nums.length; i++) {
if(nums[i]==sort[i]||uf.find(nums[i])==uf.find(sort[i])) continue;
return false;
}
return true;
}
class UnionFind {
int[] nums;
int[] ss;
UnionFind(int n) {
nums = new int[n];
ss = new int[n];
for (int i = 0; i < n; i++) {
nums[i] = i;
}
}
public int find(int t){
if(nums[t]!=t) nums[t] = find(nums[t]);
return nums[t];
}
public void union(int x,int y){
int a=find(x);
int b=find(y);
if(a==b) return;
if(ss[a]<ss[b]){
nums[a]=b;
}else if(ss[a]>ss[b]){
nums[b]=a;
}else{
nums[b]=a;
ss[a]++;
}
}
}
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
| use std::collections::HashMap;
struct UnionFind {
parent: Vec<usize>, // 每个元素的父节点数组,用于记录连通关系
rank: Vec<usize>, // 每个集合的秩(树的深度),用于优化合并操作
}
impl UnionFind {
// 初始化并查集
fn new(size: usize) -> Self {
UnionFind {
parent: (0..size).collect(), // 初始化父节点为自身
rank: vec![0; size], // 初始化所有秩为 0
}
}
// 查找操作,路径压缩
fn find(&mut self, t: usize) -> usize {
if self.parent[t] != t {
self.parent[t] = self.find(self.parent[t]); // 递归查找根节点并压缩路径
}
self.parent[t]
}
// 合并操作,按秩合并
fn union(&mut self, x: usize, y: usize) {
let root_x = self.find(x);
let root_y = self.find(y);
if root_x != root_y {
if self.rank[root_x] < self.rank[root_y] {
self.parent[root_x] = root_y;
} else if self.rank[root_x] > self.rank[root_y] {
self.parent[root_y] = root_x;
} else {
self.parent[root_y] = root_x;
self.rank[root_x] += 1; // 增加根节点 x 的秩
}
}
}
}
struct Solution;
impl Solution {
pub fn gcd_sort(nums: Vec<usize>) -> bool {
let mut sorted_nums = nums.clone(); // 创建排序后的数组
sorted_nums.sort_unstable(); // 对数组进行排序
let max_num = *nums.iter().max().unwrap(); // 找到数组中的最大值
let mut uf = UnionFind::new(max_num + 1); // 初始化并查集
// 遍历每个数字,将其与因子进行合并
for &num in &nums {
let mut t = 2;
while t * t <= num {
if num % t == 0 {
uf.union(num, t); // 合并 num 和因子 t
if num / t > 1 {
uf.union(num, num / t); // 合并 num 和因子 num/t
}
}
t += 1;
}
}
// 检查是否可以通过排序后的数组匹配原数组
for (i, &num) in nums.iter().enumerate() {
if num != sorted_nums[i] && uf.find(num) != uf.find(sorted_nums[i]) {
return false; // 如果不能匹配,返回 false
}
}
true // 如果所有数字匹配,返回 true
}
}
|
并查集的用途
并查集(Union-Find)是一种高效的数据结构,广泛用于解决动态连通性问题,尤其是在需要判断某些元素是否属于同一集合的场景。以下是它的常见应用:
1. 图论相关问题
- 连通分量:判断图中两点是否连通,以及连通分量的个数。
- 最小生成树:Kruskal 算法中用于判断是否形成环。
- 检测图中环:判断无向图是否存在环结构。
2. 网络问题
- 网络连通性:比如计算电网或通信网络中各个节点的连通状态。
- 组网问题:用于动态添加边或节点后,快速判断网络是否连通。
3. 集合相关问题
- 动态合并集合:在需要频繁合并集合或查询两个元素是否属于同一集合时效率极高。
- 分组问题:例如将不同属性的对象分为相互独立的组。
4. 动态归类问题
- 语言处理:词汇归类为语义相似的组。
- 人群归并:解决社交网络中朋友分组问题。
5. 实际案例
- 岛屿问题:例如“计算岛屿的数量”或“是否存在水陆相连的路径”。
- 模拟系统:模拟物理系统中的相互作用,比如流体或物体碰撞。
并查集的核心优点是通过路径压缩和按秩合并优化,使查询和合并的复杂度接近 O(1)。








