详细解释拓扑排序
定义
如何给一个有向无环图的所有节点排序
如果有向图中存在环,就无法进行拓扑排序
拓扑排序的步骤
- 从图中选择一个入度为零的点
- 输出该顶点,从图中删除此顶点及其所有的出边
- 重复上面两步,直到所有顶点都输出,拓扑排序完成。或图中不存在入度为零的点(图中有环),拓扑排序无法完成,进入死循环。
Kahn算法(BFS)
深度优先搜索
初始状态下,集合S装着所有入度为0的点,L是一个空列表。
每次从S中取出一个点u放入L,然后将u的所有边删除。对于边(u,v)若将该边删除后,点v的入度变为0,则将v放入S中。
不断重复以上过程,直到集合S为空。检测图中是否存在任何边,如果有,那么此图有环。否则返回L,L中顶点的顺序就是拓扑排序的结果。

对其排序的结果就是:2 -> 8 -> 0 -> 3 -> 7 -> 1 -> 5 -> 6 -> 9 -> 4 -> 11 -> 10 -> 12
时间复杂度
图G=(V,E) 一共需要遍历两遍图
总时间复杂度O(E+V)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
| int n, m;
vector<int> G[MAXN];
int in[MAXN]; // 存储每个结点的入度
bool toposort() {
vector<int> L;
queue<int> S;
for (int i = 1; i <= n; i++)
if (in[i] == 0) S.push(i);
while (!S.empty()) {
int u = S.front();
S.pop();
L.push_back(u);
for (auto v : G[u]) {
if (--in[v] == 0) {
S.push(v);
}
}
}
if (L.size() == n) {
for (auto i : L) cout << i << ' ';
return true;
}
return false;
}
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
| public class TopoSort {
static int n, m;
static List<Integer>[] G;
static int[] in; // 存储每个结点的入度
public static boolean toposort() {
//用来存放拓扑排序的结果
List<Integer> L = new ArrayList<>();
//存放入度为零的点
Queue<Integer> S = new LinkedList<>();
for (int i = 1; i <= n; i++) {
if (in[i] == 0) {
S.add(i);
}
}
while (!S.isEmpty()) {
int u = S.poll();
L.add(u);
//调整每个点的入度
for (int v : G[u]) {
if (--in[v] == 0) {
S.add(v);
}
}
}
//如果L的大小等于整个图的大小,表示图中所有点都已经被排序
if (L.size() == n) {
for (int i : L) {
System.out.print(i + " ");
}
return true;
}
//存在环
return false;
}
}
|
DFS
能BFS就一定能DFS
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
| using Graph = vector<vector<int>>; // 邻接表
struct TopoSort {
enum class Status : uint8_t { to_visit, visiting, visited };
const Graph& graph;
const int n;
vector<Status> status;
vector<int> order;
vector<int>::reverse_iterator it;
TopoSort(const Graph& graph)
: graph(graph),
n(graph.size()),
status(n, Status::to_visit),
order(n),
it(order.rbegin()) {}
bool sort() {
for (int i = 0; i < n; ++i) {
if (status[i] == Status::to_visit && !dfs(i)) return false;
}
return true;
}
bool dfs(const int u) {
status[u] = Status::visiting;
for (const int v : graph[u]) {
if (status[v] == Status::visiting) return false;
if (status[v] == Status::to_visit && !dfs(v)) return false;
}
status[u] = Status::visited;
*it++ = u;
return true;
}
};
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
| public class TopoSort {
//枚举每个点三种状态:没被访问,访问中,已访问
enum Status { TO_VISIT, VISITING, VISITED }
private final List<List<Integer>> graph;
private final int n;
private final Status[] status;
private final List<Integer> order;
public TopoSort(List<List<Integer>> graph) {
//图
this.graph = graph;
//图大小
this.n = graph.size();
//初始化每个点的状态
this.status = new Status[n];
Arrays.fill(this.status, Status.TO_VISIT);
//拓扑序
this.order = new ArrayList<>(n);
}
public boolean sort() {
for (int i = 0; i < n; i++) {
if (status[i] == Status.TO_VISIT && !dfs(i)) {
return false;
}
}
Collections.reverse(order);
return true;
}
private boolean dfs(int u) {
status[u] = Status.VISITING;
for (int v : graph.get(u)) {
if (status[v] == Status.VISITING) return false;
if (status[v] == Status.TO_VISIT && !dfs(v)) return false;
}
status[u] = Status.VISITED;
order.add(u);
return true;
}
public List<Integer> getOrder() {
return order;
}
}
|
应用
可以判定图中是否有环
判断图是否一条链
估算工程完成的最短时间。
模板
P1347 排序
题目描述
一个不同的值的升序排序数列指的是一个从左到右元素依次增大的序列,例如,一个有序的数列 $A,B,C,D$ 表示 $A<B,B<C,C<D$。在这道题中,我们将给你一系列形如 $A<B$ 的关系,并要求你判断是否能够根据这些关系确定这个数列的顺序。
输入格式
第一行有两个正整数 $n,m$,$n$ 表示需要排序的元素数量,$2\leq n\leq 26$,第 $1$ 到 $n$ 个元素将用大写的 $A,B,C,D,\dots$ 表示。$m$ 表示将给出的形如 $A<B$ 的关系的数量。
接下来有 $m$ 行,每行有 $3$ 个字符,分别为一个大写字母,一个 < 符号,一个大写字母,表示两个元素之间的关系。
输出格式
若根据前 $x$ 个关系即可确定这 $n$ 个元素的顺序 yyy..y(如 ABC),输出
Sorted sequence determined after xxx relations: yyy...y.
若根据前 $x$ 个关系即发现存在矛盾(如 $A<B,B<C,C<A$),输出
Inconsistency found after x relations.
若根据这 $m$ 个关系无法确定这 $n$ 个元素的顺序,输出
Sorted sequence cannot be determined.
(提示:确定 $n$ 个元素的顺序后即可结束程序,可以不用考虑确定顺序之后出现矛盾的情况)
输入输出样例 #1
输入 #1
1
2
3
4
5
6
7
| 4 6
A<B
A<C
B<C
C<D
B<D
A<B
|
输出 #1
1
| Sorted sequence determined after 4 relations: ABCD.
|
输入输出样例 #2
输入 #2
输出 #2
1
| Inconsistency found after 2 relations.
|
输入输出样例 #3
输入 #3
输出 #3
1
| Sorted sequence cannot be determined.
|
说明/提示
$2 \leq n \leq 26,1 \leq m \leq 600$。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
| import java.util.*;
class Main {
static int n, m, sum, ans, k, have;
static List<Integer>[] vec = new ArrayList[26];
static int[] ru = new int[26], ru2 = new int[26];
static Set<Integer> s1 = new HashSet<>();
static void make() {
Queue<Integer> q = new LinkedList<>();
int[] ru1 = new int[26];
Arrays.fill(ru1, 0);
for (int i = 0; i < 26; i++) {
for (int v : vec[i]) {
ru1[v]++;
}
}
for (int i = 0; i < 26; i++) {
if (ru1[i] == 0 && s1.contains(i)) {
q.add(i);
System.out.print((char) (i + 'A'));
}
}
while (!q.isEmpty()) {
int u = q.poll();
for (int v : vec[u]) {
ru1[v]--;
if (ru1[v] == 0) {
q.add(v);
System.out.print((char) (v + 'A'));
}
}
}
}
static void topo() {
// 记录所有可以排的节点
Queue<int[]> q = new LinkedList<>();
for (int i = 0; i < 26; i++) {
// 如果入度为0,且包含此节点,则入队
if (ru[i] == 0 && s1.contains(i)) {
q.add(new int[]{i, 1});
// 总数+1
sum++;
}
}
// 开始真正的排序
while (!q.isEmpty()) {
int[] node = q.poll();
int u = node[0], val = node[1];
for (int v : vec[u]) {
// 入度-1
ru[v]--;
// 如果入度变成0,则又有一个元素,可以排序,入队
if (ru[v] == 0) {
sum++;
q.add(new int[]{v, val + 1});
ans = Math.max(ans, val + 1);
}
}
}
if (ans == n) {
System.out.printf("Sorted sequence determined after %d relations: ", k);
make();
System.out.println(".");
System.exit(0);
}
if (sum != have) {
System.out.printf("Inconsistency found after %d relations.%n", k);
System.exit(0);
}
}
public static void main(String[] args) {
// 读取
Scanner sc = new Scanner(System.in);
// 图大小
n = sc.nextInt();
m = sc.nextInt();
// 建图
for (int i = 0; i < 26; i++) {
vec[i] = new ArrayList<>();
}
for (int i = 1; i <= m; i++) {
String s = sc.next();
k = i;
int u = s.charAt(0) - 'A';
int v = s.charAt(2) - 'A';
// u到v有一条边
vec[u].add(v);
// 存在u和v节点
s1.add(u);
s1.add(v);
// 目前共有多少个节点
have = s1.size();
// v的入度+1
ru2[v]++;
sum = 0;
ans = 0;
//
System.arraycopy(ru2, 0, ru, 0, ru2.length);
// 拓扑排序
topo();
}
// 无法排序,无法构成图
System.out.println("Sorted sequence cannot be determined.");
}
}
|
中等
给你一个正整数 n ,它表示一个 有向无环图 中节点的数目,节点编号为 0 到 n - 1 (包括两者)。
给你一个二维整数数组 edges ,其中 edges[i] = [fromi, toi] 表示图中一条从 fromi 到 toi 的单向边。
请你返回一个数组 answer,其中 answer[i]是第 i 个节点的所有 祖先 ,这些祖先节点 升序 排序。
如果 u 通过一系列边,能够到达 v ,那么我们称节点 u 是节点 v 的 祖先 节点。
示例 1:
1
2
3
4
5
6
7
8
9
10
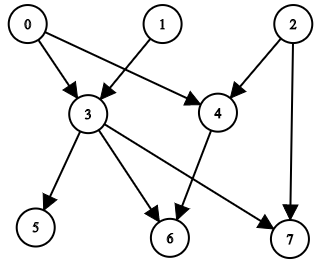
| 输入:n = 8, edgeList = [[0,3],[0,4],[1,3],[2,4],[2,7],[3,5],[3,6],[3,7],[4,6]]
输出:[[],[],[],[0,1],[0,2],[0,1,3],[0,1,2,3,4],[0,1,2,3]]
解释:
上图为输入所对应的图。
- 节点 0 ,1 和 2 没有任何祖先。
- 节点 3 有 2 个祖先 0 和 1 。
- 节点 4 有 2 个祖先 0 和 2 。
- 节点 5 有 3 个祖先 0 ,1 和 3 。
- 节点 6 有 5 个祖先 0 ,1 ,2 ,3 和 4 。
- 节点 7 有 4 个祖先 0 ,1 ,2 和 3 。
|
示例 2:
1
2
3
4
5
6
7
8
9
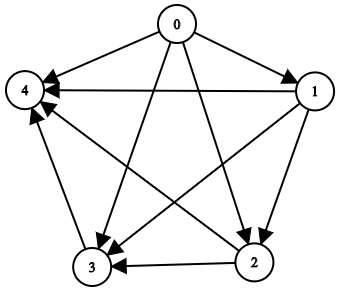
| 输入:n = 5, edgeList = [[0,1],[0,2],[0,3],[0,4],[1,2],[1,3],[1,4],[2,3],[2,4],[3,4]]
输出:[[],[0],[0,1],[0,1,2],[0,1,2,3]]
解释:
上图为输入所对应的图。
- 节点 0 没有任何祖先。
- 节点 1 有 1 个祖先 0 。
- 节点 2 有 2 个祖先 0 和 1 。
- 节点 3 有 3 个祖先 0 ,1 和 2 。
- 节点 4 有 4 个祖先 0 ,1 ,2 和 3 。
|
提示:
1 <= n <= 10000 <= edges.length <= min(2000, n * (n - 1) / 2)edges[i].length == 20 <= fromi, toi <= n - 1fromi != toi- 图中不会有重边。
- 图是 有向 且 无环 的。
拓扑排序重点需要记录哪些是没有依赖的(可以被搜索的),哪个节点的入度还有没有归零(表示当前节点还有依赖没有被搜索)。可以快速的查出,所有依赖关系和最小代价。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
| class Solution {
public List<List<Integer>> getAncestors(int n, int[][] edges) {
// 用来记录每个表的入度,当入度为0时,表示当前节点没有依赖节点,可以被搜索并返回
int[] nums=new int[n];
// 构造当前图
List<Integer>[] map=new List[n];
for (int i = 0; i < map.length; i++) {
map[i]=new ArrayList<>();
}
// 目前已经被搜索的答案
Set<Integer>[] sets=new Set[n];
for (int i = 0; i < sets.length; i++) {
sets[i]=new HashSet<>();
}
// 方法一,利用广度优先搜索来实现拓扑排序
// 表示当前可以被搜索的节点有哪些
Deque<Integer> queue=new LinkedList<>();
// 现在开始构造图
for(int[] edge:edges){
// 依赖0的节点有哪些
map[edge[0]].add(edge[1]);
// 1需要依赖0所有1的入度+1
nums[edge[1]]++;
}
// 把所有可以被搜索的数入队
for(int i=0;i<n;i++){
if(nums[i]==0) queue.offer(i);
}
// 没有孤岛,且无环
while(!queue.isEmpty()){
// 当前被搜索的节点
int t=queue.poll();
for(int a:map[t]){
// 当前节点已经搜索了a,依赖t
sets[a].add(t);
// 当前节点a依赖t的所有依赖节点
sets[a].addAll(sets[t]);
// a的一个依赖已经被理清,如果所有入度-1
nums[a]--;
// 如果a所有依赖都已经被搜索过,就可以搜索依赖a的元素
if(nums[a]==0) queue.offer(a);
}
}
// 开始构造答案,和拓扑排序本身无关
List<List<Integer>> res=new ArrayList<>();
for(int i=0;i<n;i++){
List<Integer> list=new ArrayList<>(sets[i]);
Collections.sort(list);
res.add(list);
}
return res;
}
}
|
老规矩,能rust尽量rust
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
| use std::collections::{HashSet,VecDeque};
impl Solution {
pub fn get_ancestors(n: i32, edges: Vec<Vec<i32>>) -> Vec<Vec<i32>> {
let n=n as usize;
let mut anc: Vec<HashSet<i32>> = vec![HashSet::new();n];
// 初始化List<List<Integer>>
let mut e:Vec<Vec<i32>> = vec![Vec::new();n];
// 初始化数组,默认值0,数组长度n
let mut indeg : Vec<i32> =vec![0;n];
for edge in edges{
// 向list[0] 中添加元素1
e[edge[0] as usize].push(edge[1]);
indeg[edge[1] as usize] +=1;
}
let mut q:VecDeque<i32> =VecDeque::new();
// for(int i=0;i<n;i++)
for i in 0..n{
if indeg[i]==0{
q.push_back(i as i32);
}
}
while let Some(u) = q.pop_front(){
for v in &e[u as usize]{
// 复制祖先节点集合,避免同时遍历和修改,因为所有权的关系
let mut new_ancestors= anc[* v as usize].clone();
new_ancestors.insert(u);
for i in &anc[u as usize]{
new_ancestors.insert(*i);
}
anc[*v as usize] =new_ancestors;
indeg[*v as usize]-=1;
if indeg[*v as usize]==0{
q.push_back(*v);
}
}
}
let mut res:Vec<Vec<i32>> = vec![Vec::new();n as usize];
for i in 0..n as usize{
res[i]=anc[i].iter().cloned().collect::<Vec<i32>>();
res[i].sort();
}
res
}
}
|