出处
来自307. 区域和检索 - 数组可修改 - 力扣(LeetCode)茶神的题解
动机
场景
给你一个数组,如何快速的计算任意一段连续子数组的元素和?
对于一个子数组来说,如果遍历子数组的每个数,把它们加起来,时间复杂度是 O(n),太慢了。
下标从left的right的子数组元素和,可以看成是下标从1到right的子数组元素和,减去下标从1到left-1的子数组元素和。例如数组[3,1,4,1,5,9],子数组[4,1,5]的元素和,等于[3,1,4,1,5]的元素和,减去[3,1]的元素和。
按这个方法,算出每个前缀[1,i](表示下标从1到i的连续子数组)的元素和,就可以O(1)的计算任意连续子数组的元素和了。
更新
但是,如果还可以修改数组中的元素呢?
比如我把下标为1的元素修改了,由于所有前缀都包含下标1,那么就需要更新所有前缀的元素和,更新操作就需要O(n)的时间,太慢了。
能不能把前缀[1,i]拆分成若干段连续子数组呢?
如果拆分的太细,比如拆分成[1,1],[2,2],[3,3],···,虽然更新是O(1)的,但计算子数组元素和还是得遍历累加,时间复杂度是O(n),太慢了。
平衡
上面的方法,要么询问是O(1)更新是O(n),要么询问是O(n)更新是O(1),时间差距悬殊。
如何平衡询问和更新的时间复杂度?
关键在于如何拆分子数组(区间)。
能否把任意前缀拆分成若干个关键区间,使得更新操作也只会更新若干个关键区间?
这样回答询问时,只需要遍历并累加若干个关键区间的元素和。更新元素时,也只需要遍历并更新若干个关键区间的元素和。
如何拆分?
启示:如果把一个正整数i拆分成若干个不同的2的幂(从大到小),那么只会拆分出O(logi)个数。前缀能否也这样拆分?
举个例子,13=8+4+1,那么前缀[1,13]可以拆分成三个长度分别为8,4,1的关键区间:[1,8],[9,12],[13,13]。
按照这个规则,来看看从[1,1]到[1,8]是如何拆分的:
| [1,1]=[1,1] | (1=1) |
|---|---|
| [1,2]=[1,2] | (2=2) |
| [1,3]=[1,2]+[3,3] | (3=2+1) |
| [1,4]=[1,4] | 4=4 |
| [1,5]=[1,4]+[5,5] | 5=4+1 |
| [1,6]=[1,4]+[5,6] | 6=4+2 |
| [1,7]=[1,4]+[5,6]+[7,7] | 7=4+2+1 |
| [1,8]=[1,8] | 8=8 |
数一数,按照这种拆分方式,一共有多少个不同的关键区间?
有8个:[1,1],[1,2],[3,3],[1,4],[5,5],[5,6],[7,7],[1,8]。
- 如果i是2的幂,那么[1,i]无需拆分。
- 如果i不是2的幂,先拆分出一个最小的2的幂,记作lowbit(i)(例如6拆分出2),得到长为lowbit(i)的关键区间[i-lowbit(i)+1,i],问题就转换成剩下的[1,i-lowbit(i)]如何拆分,这是一个规模更小的子问题。
总共有n个不同的关键区间。
证明
按顺序拆分前缀[1,1],[1,2],[1,3],···,[1,n],每个只会恰好拆出一个新的关键区间[i-lowbit(i)+1,i](注意[1,i-lowbit(i)]之前拆分过了,不会产生新的关键区间),所以一共有n个不同的关键区间。
算法
由于关键区间的右端点互不相同,我们可以把右端点为i的关键区间的元素和保存在tree[i]中。
按照如下的方法计算前缀[1,i]的元素和:
- 初始化元素和s=0.
- 每次循环,把tree[i]加到s中,对应关键区间[i-lowbit(i)+1,i]的元素和。
- 然后更新i为i-lowbit(i),表示接下来要拆分[1,i-lowbit(i)],获取其中关键区间的元素和。
- 循环直到i=0为止。
- 返回s。
由于正整数i的二进制长度是 [log2i]+1,所以任意前缀至多拆分出O(logN)个关键区间,所以上述算法的时间复杂度为O(logN)。
关于lowbit(i)的计算方法,请看从集合论到位运算,常见位运算技巧分类总结!。
要计算sumRange(left,right),可以分别计算[1,right+1]的元素和(改成下标从1开始),以及[1,left]的元素和,两者相减即为答案。
如何更新
假如下标x发生了更新,那么所有包含x的关键区间都会被更新。
例如下标5更新了,那么关键区间[5,5],[5,6],[1,8],[1,16]都需要更新,这三个关键区间的右端点依次为5,6,8,16。
如果在5-6,6-8,8-16之间连边(其它位置也同理),我们可以得到一个什么样的结构?
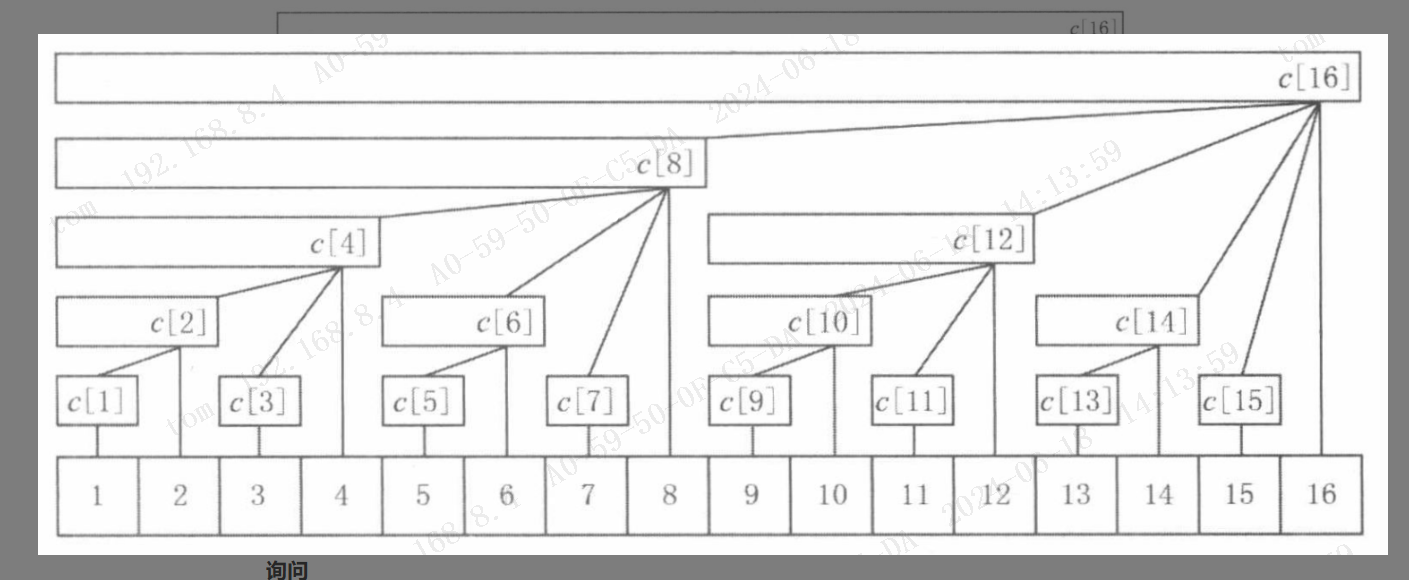
如下图,这些关键区间可以形成如下树形结构(区间元素好保存在区间右端点处)。
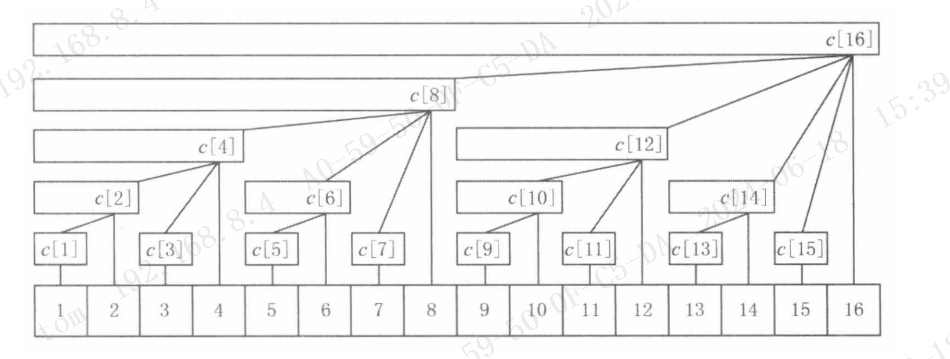
注意到:
5+lowbit(5)=5+1=6
6+lowbit(6)=6+2=8
8+lowbit(8)=8+8=16
猜想:
如果x是一个被更新的关键区间的右端点,那么下一个被更新的关键区间的右端点为x+lowbit(x)。
我们需要证明两点:
- 右端点为x的关键区间,被右端点为x+lowbit(x)的关键区间包含。
- 右端点在[x+1,x+lowbit(x)-1]内的关键区间,与右端点为x的关键区间没有任何交集。
1的证明
设y=x+lowbit(x),由于y>x,我们只需要证明这两个关键区间的左端点满足
y-lowbit(y)+1<=x-lowbit(x)+1
即 y-lowbit(y)<=x-lowbit(x) 就能证明包含关系。 设lowbit(x)=2^k,那么x=m*2^(k+1)+2^k,这里m是一个非负整数。 所以不等式右边为
x−lowbit(x)=m⋅2
k+1
由于 y=x+lowbit(x)=(m+1)⋅2k+1y=x+\text{lowbit}(x)=(m+1)\cdot 2^{k+1}y=x+lowbit(x)=(m+1)⋅2 k+1 ,得到 lowbit(y)≥2k+1\text{lowbit}(y)\ge 2^{k+1}lowbit(y)≥2 k+1 ,
所以不等式左边为
y−lowbit(y)≤m⋅2k+1y-\text{lowbit}(y) \le m\cdot 2^{k+1} y−lowbit(y)≤m⋅2 k+1
综上所述
y−lowbit(y)≤m⋅2k+1=x−lowbit(x)y-\text{lowbit}(y)\le m\cdot 2^{k+1} = x-\text{lowbit}(x) y−lowbit(y)≤m⋅2 k+1 =x−lowbit(x) 这说明包含关系是成立的。
2的证明
设y=x+b,其中1<=b<2^k(k的定义同上)。 右端点为y的关键区间,左端点为y-lowbit(y)+1。我们只需要证明 y-lowbit(y)+1>x 就能证明右端点为y的关键区间,一定在右端点为x的关键区间的右侧,他们没有任何任何交集的。
算法
对于update(index,val),算法如下:
- 设delta=val-nums[index],相当于把index的元素增加了这么多。然后把nums[index]更新成val。
- 初始化i=index+1(注意下标从1开始),这是第一个被更新的关键区间右端点。
- 不断的循环直到i>n,这里n是nums的长度。
- 每次循环,把tree[i]增加delta。
- 然后更新i为i+lowbit(i),